ex. 5*5*5=5³
Just like all of math though, you have to be aware of the rules that come with exponents. There are some basic rules of exponents:
1st: To try to simplify or do any of the following, the base number must be the same. So in our examples below our base is a.
(a4)(b3) = aaaabbb = (a4)(b3). Nothing combines.
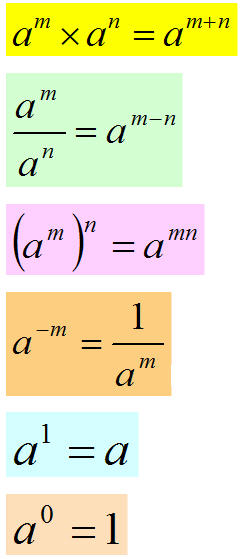
3rd: When dividing powers with the same base we subtract the exponents.
4th: When you have an exponent expression that is raised to a power, you can multiply the exponent and the power.
5th: If the power contains a negative exponent, rewrite the expression with a positive exponent by taking the reciprical.
6th: We said "The exponent represents how many times it will be multiplied by itself. When your base number is to the first power it is ALWAYS the base numer.
7th: Anything to the power of zero is ALWAYS "1"
I got my clip art from: http://www.math-play.com/exponent-game.html